FRAKTAL SEGITIGA SIERPINSKI
FRAKTAL SEGITIGA SIERPINSKI
Dengan menyebut nama Allah Yang Maha Pengasih Lagi Maha Penyayang pada kesempatan ini akan
mengungkap sedikit tentang Segitiga Sierspinki yang kurang disadari akan keberadaannya.
Segitiga Sierpinski merupakan segitiga yang terus membagi dirinya dengan menggunakan segitiga-segitiga lain
yang mirip namun dengan skala yang terus berbeda.
Segitiga Sierpinski merupakan salah satu contoh dari fraktal. Istilah fraktal diberikan oleh Benoit Mandelbrot
tahun 1975 dan diturunkan dari bahasa latin, fractus yang berarti “pecah” atau “patah” fraktal matematika
didasarkan pada persamaan iterasi, semacam umpan balik berdasarkan rekursif.
mengungkap sedikit tentang Segitiga Sierspinki yang kurang disadari akan keberadaannya.
Segitiga Sierpinski merupakan segitiga yang terus membagi dirinya dengan menggunakan segitiga-segitiga lain
yang mirip namun dengan skala yang terus berbeda.
Segitiga Sierpinski merupakan salah satu contoh dari fraktal. Istilah fraktal diberikan oleh Benoit Mandelbrot
tahun 1975 dan diturunkan dari bahasa latin, fractus yang berarti “pecah” atau “patah” fraktal matematika
didasarkan pada persamaan iterasi, semacam umpan balik berdasarkan rekursif.
Walaupun fraktal adalah konstruksi matematis, ia ditemukan dialam yang membawa pada penerapannya
dalam bidang seni. Ia juga berguna dalam kedokteran, mekanika tanah, seismologi dan analis teknik.
Salah satu jenis fraktal yang dikenal ialah Segitiga Sierpinski.
Sesuai dengan namanya, Segitiga Sierpinski digambarkan untuk pertama kali oleh seorang matematikawan
Waclaw Polandia.
Sierpinski ini dibuat pada tahun 1915 melalui metode rekursif pada segitiga utama tiap sisinya dibagi dua
untuk membuat titik-titik baru, kemudian dari ketiga sisi yang terbentuk saling dihubungkan menjadi sebuah
segitiga yang lebih kecil.
dalam bidang seni. Ia juga berguna dalam kedokteran, mekanika tanah, seismologi dan analis teknik.
Salah satu jenis fraktal yang dikenal ialah Segitiga Sierpinski.
Sesuai dengan namanya, Segitiga Sierpinski digambarkan untuk pertama kali oleh seorang matematikawan
Waclaw Polandia.
Sierpinski ini dibuat pada tahun 1915 melalui metode rekursif pada segitiga utama tiap sisinya dibagi dua
untuk membuat titik-titik baru, kemudian dari ketiga sisi yang terbentuk saling dihubungkan menjadi sebuah
segitiga yang lebih kecil.
Sehingga terbentuk 3 segitiga dipinggir dan satu segitiga paling besar di tengah. Demikian seterusnya untuk segitiga-segitiga yang terletak di pinggir/sudut segitiga besar dilakukan proses serupa. Perhatikan Gambar di bawah ini.
Dari gambar di atas dapat diketahui banyaknya segitiga pada suku ke-n (Un), jumlah banyaknya segitiga pada suku ke-n (Sn), panjang benang yang dibutuhkan untuk membuat segitiga pada suku ke-n (Un), jumlah panjang benang yang dibutuhkan untuk membuat segitiga pada suku ke-n (Sn), luas segitiga terkecil pada suku ke-n (Un), jumlah luas segitiga terkecil pada suku ke-n (Sn) serta pembuktian secara induksi pada masing-masing Un dan Sn. Untuk lebih jelasnya perhatikan uraian berikut.
- Banyaknya segitiga pada suku ke-n (Un)
Dari Segitiga Sierpinski diperoleh data U1, U2, U3 s.d. Un untuk banyaknya segitiga pada setiap segitiga, sebagai berikut :
U1 U2 U3 U4 Un
1 , 5 , 17 , 53 , Un
Adapun untuk mencari rumus suku ke-n (Un) diasumsikan pada sebuah pola di bawah ini:
1 + 4 + 12 + 36 + 108 + . . . + N
* N adalah bilangan bulat, hasil dari 3 dikali bilangan sebelumnya
dari pola tersebut, dapat diambil sebuah kesimpulan bahwa setelah bilangan pertama yakni dari bilangan ke-2 sampai dengan seterusnya memiliki sebuah rasio yaitu 3 (r = 3). Bilangan pertama dikesampingkan dahulu untuk memperoleh sebuah pola sebagai berikut
4 + 12 + 36 + 108 + . . . + N
Setelah dikesampingkan bilangan yang pertama yaitu 1, kita bisa memperoleh sebuah rumus suku ke-n (Un) dengan menggunakan rumus jumlah ke-n (Sn) yaitu ;
Sn = a (rn – 1) , r ≥ 1
r – 1
alasan menggunakan rumus jumlah ke-n (Sn) yaitu pemisah dari pola tersebut ialah tambah (+) bukan koma (,). Pola di atas memiliki r = 3 serta a = 4, jadi diperoleh :
Sn = 4(3n – 1) = 4(3n – 1) = 2(3n – 1)
3-1 2
Jadi, 1 + 4 + 12 + 36 + 108 + . . . + N = 1 + 2(3n – 1). Karena 1 + 4 + 12 + 36 + 108 + . . . + N asumsi dari 1, 5, 17, 53, 161 . . . Un, maka
Un = 1 + 2(3n – 1)
Hanya saja apabila mencari U1 hasilnya tidak sesuai dengan pola, begitu juga dengan U2, U3, dan seterusnya. apabila dibuktikan sebagai berikut ;
- U1 = 1+2(31-1)
= 1+2(2)
= 1+4
= 5
- U2 = 1+2(32-1)
= 1+2(8)
= 1+16
= 17
- U3 = 1+2(33-1)
= 1+2(26)
= 1+52
= 53
setelah melalui berbagai cara, kemudian diasumsikan bahwa rumus untuk banyaknya segitiga pada suku ke-n (Un) yang tepat ialah
Un = 1 + 2(3n-1 – 1)
kebenaran tersebut dapat dibuktikan, sebagaimana di bawah ini ;
- U1 = 1+2(31-1-1)
= 1+2(30-1)
= 1+2(1-1)
= 1+2(0)
= 1+0
= 1
- U2 = 1+2(32-1-1)
= 1+2(3-1)
= 1+2(2)
= 1+4
= 5
- U3 = 1+2(33-1-1)
= 1+2(32-1)
= 1+2(9-1)
= 1+2(8)
= 1+16
=17
- U4 = 1+2(34-1-1)
= 1+2(33-1)
= 1+2(27-1)
= 1+2(26)
= 1+52
= 53
- Jumlah banyaknya segitiga pada suku ke-n (Sn)
1 + 5 + 17 + 53 + . . . + Un
Dari barisan deret di atas, bisa diperoleh rumus untuk jumlah banyaknya segitiga ke-n (Sn) pada suku ke-n (Un) yaitu Sn = 3.3n-1 – n – 1
Rumus tersebut bisa diperoleh dengan menganggap bahwa Sn = U1 + U2 + U3 + U4 + . . . + Un , berarti
Sn = 1+2(30-1) + 1+2(31-1) + 1+2(32-1) + 1+2(33-1) + . . . + 1+2(3n-1-1)
Apabila kita uraikan mulai dari S1, S2, S3 dan seterusnya maka ;
- S1 = 1+2(30-1)
= 1+2(0)
= 1+0
= 1
- S2 = 1+2(30-1) + 1+2(31-1)
= 2+2(31-1)
- S3 = 1+2(30-1) + 1+2(31-1) + 1+2(32-1)
= 3+2(31+32-2)
- S4 = 1+2(30-1) + 1+2(31-1) + 1+2(32-1) + 1+2(33-1)
= 4+2(31+32+33-3)
Dari uraian di atas dapat diduga bahwa rumus jumlah banyaknya segitiga ke-n (Sn) pada suku ke-n (Un) ialah Sn = n + 2[ 3/2(3n-1-1) – (n-1) ]. Jikalau diuraikan akan menjadi ;
Sn = n + 2[ 3/2(3n-1-1) – (n-1) ]
= n + 2.3/2(3n-1-1) – 2(n-1)
= n + 3(3n-1-1) – 2n +2
= n + 3.3n-1 – 3 – 2n + 2
= 3.3n-1 – n – 1
- Pembuktian Secara Induksi dari 1 + 5 + 17 + 53 + . . . + 1+2(3n-1-1) = 3.3n-1 – n – 1
Rumus banyaknya segitiga pada suku ke-n (Un) serta jumlah banyaknya segitiga pada suku ke-n (Sn) yang sudah diketahui bisa dibuktikan kebenarannya dengan induksi matematika, sebagai berikut.
1 + 5 + 17 + 53 + . . . + 1+2(3n-1-1) = 3.3n-1 – n – 1
Bukti :
- misalkan p(n) menyatakan 1 + 5 + 17 + 53 + . . . + 1+2(3n-1-1) = 3.3n-1 – n – 1
p(1) ialah
1+2(31-1-1) = 3.31-1 – 1 – 1
1+2(30-1) = 3.30 – 1 – 1
1+0 = 3 – 2
1 = 1
Pernyataan benar.
- Diasumsikan bahwa p(k) benar untuk suatu bilangan asli k, yaitu :
1 + 5 + 17 + 53 + . . . + 1+2(3k-1-1) = 3.3k-1 – k – 1, pernyataan benar.
Selanjutnya harus ditunjukkan bahwa p(k+1) benar, yaitu :
1 + 5 + 17 + 53 + . . . + 1+2(3k-1-1) + 1+2(3k-1) = 3.3k – k – 2
Hal ini ditunjukkan sebagai berikut :
1 + 5 + 17 + 53 + . . . + 1+2(3k-1-1) + 1+2(3k-1) = [1 + 5 + 17 + 53 + . . . + 1+2(3k-1-1)] + 1+2(3k-1)
= 3.3k-1 – k – 1 + 1+2(3k-1)
= 3.3k-1 – k – 1 + 1+ 2.3k – 2
= 3.3k.3-1 – k – 1 +1 + 2.3k – 2
= 3.3k - k – 2
Ternyata 1 + 5 + 17 + 53 + . . . + 1+2(3k-1-1) + 1+2(3k-1) = 3.3k – k – 2 untuk p(k+1) pernyataan benar. Sehingga p(n) benar untuk setiap bilangan asli n
- Panjang benang yang dibutuhkan pada suku ke-n (Un)
Gambar Sierpinski di atas memberikan sebuah pola, untuk menentukan panjang benang yang dibutuhkan pada suku ke-n (Un)
3 , 4.5 , 6.75 , 10.125 , . . . , Un
Dapat diambil sebuah kesimpulan bahwa pola tersebut memiliki a = 3 serta r = 32. jadi rumus yang diperoleh ialah
Un = a.rn-1
= 3.(3/2)n-1
- Jumlah panjang benang yang dibutuhkan pada suku ke-n (Sn)
3 + 4.5 + 6.75 + 10.125 + . . . + Un
Sn = a (rn-1)r-1 , r ≥1
= 3 [(32)n-1]32-1
= 3 [(32)n-1]32-22
= 3 [(32)n-1]12
= 6 [(32)n-1]
- Pembuktian secara induksi dari 3 + 4.5 + 6.75 + 10.125 + . . . + 3.(3/2)n-1 = 6 [(32)n-1]
3 + 4.5 + 6.75 + 10.125 + . . . + 3.(3/2)n-1 = 6 [(32)n-1]
Bukti :
- Misalkan p(n) menyatakan 3 + 4.5 + 6.75 + 10.125 + . . . + 3.(3/2)n-1 = 6 [(32)n-1]
P(1) ialah 3.(3/2)n-1 = 6 [(32)n-1]
3.(3/2)1-1 = 6 [(32)1-1]
3.(3/2)0 = 6 [32-1]
3.1 = 6 [12]
3 = 3
Pernyataan benar untuk p(1).
- Diasumsikan bahwa p(k) benar untuk suatu bilangan asli k, yaitu :
3 + 4.5 + 6.75 + 10.125 + . . . + 3.(3/2)k-1 = 6 [(32)k-1], pernyataan benar
Selanjutnya harus ditunjukkan bahwa p(k+1) benar, yaitu :
3 + 4.5 + 6.75 + 10.125 + . . . + 3.(3/2)k-1 + 3.(3/2)k = 6 [(32)k+1-1]
Hal ini ditunjukkan sebagai berikut :
[3 + 4.5 + 6.75 + 10.125 + . . . + 3.(3/2)k-1] + 3.(3/2)k = 6 [(32)k-1] + 3.(3/2)k
= 6(32)K-6+3.3K2K
= 6.3K2K+3.3K2K-6
= 9.3K2K-6
= 6 [(32)k+1-1]
Ternyata 3 + 4.5 + 6.75 + 10.125 + . . . + 3.(3/2)k-1 + 3.(3/2)k = 6 [(32)k+1-1] untuk p(k+1) pernyataanya benar. Sehingga p(n) benar untuk setiap bilangan asli n.
- Luas sebuah segitiga terkecil pada suku ke-n (Un)
Dari Segitiga Sierpinski yang diketahui dengan panjang rusuk setiap sisi sama yaitu 1 cm maka bisa diperoleh luas segitiga terkecil hasil dari iterasi. Misal setiap sudut sisi itu terdiri dari titik A, titk B serta titik C, dengan AB = BC = CA = 1cm dan O adalah titi potong yang tegak lurus dari perpanjangan garis dari titik C. Berarti tinggi dari segitiga tersebut bisa diperoleh dengan menggunakan teorema phytagoras.
OC= (AC)2-(AO)2= 12-(12)2=1-14=34=123
Apabila diperhatikan, bahwa tinggi segitiga terkecil dari segitiga sierpinski selalu dibagi 2 dari tinggi sebelumnya. Hal ini karena pembuatan segitiga selanjutnya hasil dari membagi dua tiap sisi segitiga utama, kemudian dihubungkan oleh suatu garis yang menghasilkan segitiga baru serta alas segitiga yang baru setengah dari segitiga sebelumnya. Jika dibentuk dalam sebuah pola untuk Un tingginya tn.
U1 U2 U3 U4 . . . Un
t1 t2 t3 t4 . . . tn
123 143 183 1163 . . . 12n3
Sekarang akan mencari luas sebuah segitiga terkecil pada suku ke-n (Un).
L1 =12.1.123 =143
L2 =12.12.1223=1163
L3 =12.14.1233=1643 , dan seterusnya.
Maka diperoleh rumus luas sebuah segitiga terkecil pada suku ke-n (Un) ialah
Un = Ln=14n3
- Jumlah luas sebuah segitiga terkecil pada suku ke-n (Sn)
Uraian di atas dapat dibuat sebuah deret, untuk menentukan jumlah luas segitiga terkecil pada suku ke-n (Sn).
143+1163+1643+12563+…+14n3
Jika diperhatikan, deret tersebut memiliki a = 143 serta r = 14. Diperoleh rumus Sn sebagai berikut :
Sn=a(1-rn)1-r=143[1-(14)n]1-14=143[1-(14)n]1-14=143[1-(14)n]3 .14=133[1-(14)n]
Jadi, rumus jumlah luas sebuah segitiga terkecil pada suku ke-n (Sn) ialah
Sn=133[1-(14)n]
- Pembuktian secara induksi dari 143+1163+1643+12563+…+14n3= 133[1-(14)n]
143+1163+1643+12563+…+14n3= 133[1-(14)n]
Bukti :
- Misalkan p(n) menyatakan 143+1163+1643+12563+…+14n3= 133[1-(14)n]
P(1) ialah 1413= 133[1-(14)1]
143 = 133[1-14]
143 = 133[34]
143 = 143 . pernyatan benar.
- Diasumsikan bahwa p(k) benar untuk suatu bilangan asli k, yaitu :
143+1163+1643+12563+…+14k3= 133[1-(14)k], pernyataan benar.
Selanjutnya harus ditunjukkan bahwa p(k+1) benar, yaitu :
143+1163+1643+12563+…+14k3+14k+13= 133[1-(14)k+1]
Hal ini ditunjukkan sebagai berikut :
143+1163+1643+12563+…+14k3+14k+13=[143+1163+1643+12563+…+14k3]+14k+13
= 133[1-(14)k]+14k+13
= 133+[-13(14)k+14k+1]3
= 133+[14k+1-13(14)k]3
= 133+[14k.4-1.1k3.4k]3
= 133+[3.4k-4.4k12.4k.4k]3
= 133+[-4k12.4k.4k] 3
= 133+[-112.4k.1k1k]3
= 133+[-1k3.4.4k]3
= 133+[-13.1.1k4k+1]3
= 133+[-13.1k+14k+1]3
= 133+[-13.(14)k+1]3
= 133-133. (14)k+1
= 133[1-(14)k+1]
Ternyata,
143+1163+1643+12563+…+14k3+14k+13=[143+1163+1643+12563+…+14k3]+14k+13
Untuk p(k+1) pernyataannya benar. Sehingga p(n) benar untuk setiap bilangan asli n.
Uraian di atas dapat ditarik sebuah kesimpulan bahwa sebuah fraktal bisa menghasilkan sebuah motif batik yang indah dan berciri khas. Fraktal merupakan benda geometris yang kasar pada segala skala, dan terlihat dapat “dibagi-bagi” dengan cara yang radikal. Beberapa fraktal bisa dipecah menjadi beberapa bagian yang semuanya mirip dengan fraktal aslinya. Suatu fraktal bisa diperoleh banyaknya bangun lain, hasil dari iterasi bangun pertama. Selain batik, ada banyak fraktal yang ada di sekitar kita. Baik yang alami ataupun yang buatan. Sebagai contoh, daun pakis juga merupakan fraktal alami. Contoh lainnya adalah efek dari musik yang biasanya ditampilkan di software pemutar musik.
Fraktal memiliki banyak sekali macamnya, bagi para pembaca apabila ingin sekali menemukan hal yang baru selain dari Segitiga Sierpinski masih terbuka lebar. Oleh karena itu, pembaca diharapkan mampu menemukan hal baru baik yang berhubungan dengan Segitiga Sierpinski maupun yang lainnya. Mudah-mudahan dari tulisan ini dapat menjadi penyemangat bagi pembaca untuk melakukan penelitian dalam dunia matematika.
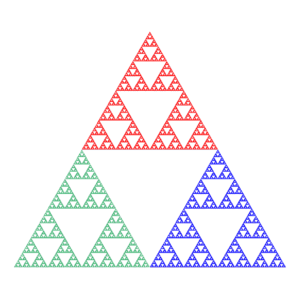
Segitiga Sierpinski, suatu fraktal, bisa dipecah menjadi tiga segitiga Sierpinski (masing-masing diberi warna berbeda).
Fraktal adalah benda geometris yang kasar pada segala skala, dan terlihat dapat "dibagi-bagi" dengan cara yang radikal. Beberapa fraktal bisa dipecah menjadi beberapa bagian yang semuanya mirip dengan fraktal aslinya. Fraktal dikatakan memiliki detail yang tak hingga dan dapat memiliki struktur serupa diri pada tingkat perbesaran yang berbeda. Pada banyak kasus, sebuah fraktal bisa dihasilkan dengan cara mengulang suatu pola, biasanya dalam proses rekursif atau iteratif.
Bahasa Inggris dari fraktal adalah fractal. Istilah fractal dibuat oleh Benoît Mandelbrot pada tahun 1975 dari kata Latin fractus yang artinya "patah", "rusak", atau "tidak teratur". Sebelum Mandelbrot memperkenalkan istilah tersebut, nama umum untuk struktur semacamnya (misalnya bunga salju Koch) adalah kurva monster.
Berbagai jenis fraktal pada awalnya dipelajari sebagai benda-benda matematis. Geometri fraktal adalah cabang matematika yang mempelajari sifat-sifat dan perilaku fraktal. Fraktal bisa membantu menjelaskan banyak situasi yang sulit dideskripsikan menggunakan geometri klasik, dan sudah cukup banyak diaplikasikan dalam sains, teknologi, dan seni karya komputer. Dulu ide-ide konseptual fraktal muncul saat definisi-definisi tradisional geometri Euklides dan kalkulus gagal menganalisis objek-objek kurva monster tersebut.
Daftar isi
Sejarah
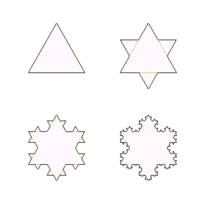
Bunga salju Koch adalah gabungan dari daerah-daerah berbentuk segitiga yang jumlahnya tak hingga. Setiap kali segitiga baru ditambahkan saat membangun bunga salju Koch (suatu iterasi), kelilingnya bertambah. Keliling bunga salju Koch adalah tak hingga.
Kontribusi dari analisis klasik
Benda-benda yang sekarang disebut fraktal sudah ditemukan dan dipelajari jauh sebelum kata fraktal muncul. Pada tahun 1872 Karl Theodor Wilhelm Weierstrass menemukan contoh fungsi dengan sifat yang tidak intuitif yaitu kontinyu di manapun namun tidak terdiferensiasi di manapun — grafik dari fungsi tersebut akan disebut fraktal pada masa sekarang. Pada tahun 1904 Helge von Koch, tidak puas dengan definisi Weierstrass yang sangat abstrak dan analitis, memberikan definisi yang lebih geometris untuk fungsi yang mirip, yang sekarang disebut bunga salju Koch. Ide mengenai kurva-kurva serupa diri dikembangkan lebih jauh oleh Paul Pierre Lévy, yang mengenalkan kurva fraktal baru bernama kurva Lévy C dalam tulisannya pada tahun 1938 berjudul Plane or Space Curves and Surfaces Consisting of Parts Similar to the Whole.
Georg Cantor memberi contoh tentang berbagai himpunan bagian dari garis riil dengan sifat yang tidak wajar — himpunan Cantor tersebut juga sekarang dikenal sebagai fraktal. Fungsi teriterasi di bidang kompleks telah diselidiki pada akhir abad 19 dan awal abad 20 oleh Henri Poincaré, Felix Klein, Pierre Fatou, dan Gaston Julia. Namun tanpa bantuan grafika komputer modern, mereka tidak dapat melihat keindahan visual benda-benda yang mereka temukan.
Aspek dari deskripsi himpunan
Dalam usahanya untuk memahami benda-benda seperti himpunan Cantor, matematikawan seperti Constantin Carathéodory dan Felix Hausdorff menggeneralisasi konsep intuitif dimensi agar memungkinkan nilai nonbulat. Ini termasuk bagian dari gerakan di pertengahan awal abad kedua puluh yang bertujuan menciptakan teori himpunan deskriptif, yaitu kelanjutan dari arah riset Cantor yang dapat mengklasifikasi himpunan titik-titik pada ruang Euclid. Definisi dimensi Hausdorff secara alami adalah geometris, walaupun didasarkan pada perkakas dari analisis matematis. Pendekatan ini digunakan oleh beberapa orang termasuk Besicovitch, yang berbeda dengan investigasi logis yang membangun sebagian besar teori himpunan deskriptif masa 1920-an dan 1930-an. Kedua bidang tersebut ditelusuri selama beberapa waktu setelahnya, terutama oleh para spesialis.
Kontribusi Mandelbrot
Pada tahun 1960-an Benoît Mandelbrot mulai menyelidiki keserupa dirian dalam berbagai tulisannya seperti How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Penyelidikannya merupakan pengembangan dari penelitian Lewis Fry Richardson. Dengan pendekatan yang sangat visual, Mandelbrot mendapatkan hubungan dari berbagai topik matematika yang sebelumnya tidak berkaitan. Pada tahun 1975, Mandelbrot menggunakan kata fractal untuk mendeskripsikan benda-benda serupa diri yang tidak memiliki dimensi yang jelas. Dia menurunkan kata fractal dari kata Latin fractus yang artinya "patah", "rusak", atau "tidak teratur". Kata fractal bukan diturunkan dari kata fractional (pecahan), seperti yang dipercaya banyak orang. Kata fractional sendiri juga diturunkan dari fractus.
Setelah visualisasi komputer diaplikasikan pada geometri fraktal, dapat disajikan argumen-argumen visual nan ampuh untuk menunjukkan bahwa geometri fraktal menghubungkan banyak bidang matematika dan sains, jauh lebih besar dan luas dari yang sebelumnya diperkirakan. Bidang-bidang yang terhubungkan oleh geometri fraktal terutama adalah dinamika nonlinier, teori chaos, dan kompleksitas. Salah satu contoh adalah menggambar metode Newton sebagai fraktal yang ternyata menunjukkan bahwa batas antara penyelesaian yang berbeda adalah fraktal dan penyelesaiannya sendiri adalah atraktor aneh. Geometri fraktal juga telah digunakan untuk kompresi data dan memodel sistem geologis dan organis yang kompleks, seperti pertumbuhan pohon dan perkembangan lembah sungai.
Pengelompokan
Fraktal bisa dikelompokkan menjadi tiga kategori luas. Pengelompokan berikut didasarkan pada cara pendefinisian atau pembuatannya.
- Sistem fungsi teriterasi — Contohnya adalah himpunan Cantor, karpet Sierpinski, kurva Peano, bunga salju Koch, kurva naga Harter-Heighway, Kotak T, dan spons Menger.
- Fraktal waktu lolos — Contohnya adalah himpunan Mandelbrot dan fraktal Lyapunov.
- Fraktal acak — Dihasilkan melalui proses stokastik, misalnya landskap fraktal dan penerbangan Lévy.
Fraktal juga bisa dikelompokkan berdasarkan keserupa diriannya. Ada tiga tingkat keperupadirian pada fraktal:
- Serupa diri secara persis — Ini adalah keserupa dirian yang paling kuat. Fraktalnya terlihat sama persis pada berbagai skala. Fraktal yang didefinisikan oleh sistem fungsi teriterasi biasanya bersifat serupa diri secara persis.
- Serupa diri secara lemah — Ini adalah keserupa dirian yang tidak terlalu ketat. Fraktalnya terlihat mirip (tapi tidak persis sama) pada skala yang berbeda. Fraktal jenis ini memuat salinan dirinya sendiri dalam bentuk yang terdistorsi maupun rusak.
- Serupa diri secara statistik — Ini adalah kererupadirian yang paling lemah. Fraktalnya memiliki ukuran numeris atau statistik yang terjaga pada skala yang berbeda. Kebanyakan definisi fraktal yang wajar secara trivial mengharuskan suatu bentuk keserupa dirian statistik. Dimensi fraktal sendiri adalah ukuran numeris yang nilainya terjaga pada berbagai skala. Fraktal acak adalah contoh fraktal yang serupa diri secara statistik, tetapi tidak serupa diri secara persis maupun lemah.
Perlu dicatat bahwa tidak semua benda yang serupa diri adalah fraktal — misalnya garis riil (garis Euclid lurus) bersifat serupa diri, tetapi argumen bahwa benda-benda Euclid adalah fraktal merupakan minoritas. Mandelbrot berargumen bahwa definisi "fraktal" sepatutnya menyertakan tidak hanya fraktal "sebenarnya", namun juga benda-benda Euclid tradisional, karena bilangan irasional di garis bilangan memiliki sifat-sifat kompleks dan tidak berulang.
Karena fraktal memiliki detail yang tak terhingga, tidak ada benda alami yang merupakan fraktal. Namun pada skala yang terbatas benda-benda alam bisa menampakkan sifat-sifat fraktalnya.
Definisi
Karakteristik fraktal, walaupun mudah dimengerti secara intuitif, ternyata sangat susah untuk dibuat definisi matematisnya. Mandelbrot mendefinisikan fraktal sebagai "himpunan yang dimensi Hausdorff Besicovitchnya lebih besar dari dimensi topologisnya". Untuk fraktal yang serupa diri secara persis, dimensi Hausdorffnya sama dengan dimensi Minkowsi Bouligandnya.
Masalah-masalah yang dihadapi saat mendefinisikan fraktal termasuk:
- Tidak ada definisi matematis dari "terlalu tidak teratur".
- Tidak ada definisi tunggal mengenai "dimensi".
- Suatu benda dapat bersifat serupa diri dengan berbagai cara.
- Tidak setiap fraktal didefinisikan secara rekursif.
Contoh
Pohon dan pakis adalah contoh fractal di alam dan dapat dimodel pada komputer menggunakan algoritme rekursif. Sifat rekursifnya bisa dilihat dengan mudah — ambil satu cabang dari suatu pohon dan akan terlihat bahwa cabang tersebut adalah miniatur dari pohonnya secara keseluruhan (tidak sama persis, tetapi mirip).
Contoh yang relatif sederhana adalah himpunan Cantor, di mana selang terbuka yang pendek dan semakin pendek tersebar pada selang dasar [0, 1], menyisakan himpunan yang mungkin serupa diri, dan mungkin memiliki dimensi d yang memenuhi 0 < d < 1. Suatu resep sederhana, yaitu menghilangkan digit 7 dari ekspansi desimal, menghasilkan himpunan Cantor yang serupa diri pada perbesaran lipat 10.
Secara umum fraktal bentuknya tidak teratur (tidak halus), jadi bukan termasuk benda yang terdefinisikan oleh geometri tradisional. Ini berarti bahwa fraktal cenderung memiliki detail yang signifikan, terlihat dalam skala berapapun; saat ada keserupa dirian, ini bisa terjadi karena memperbesar fraktal tersebut akan menunjukkan gambar yang mirip. Himpunan-himpunan tersebut biasanya didefinisikan dengan rekursi.
Sebagai perbandingan, ambil benda Euklid biasa, misalnya lingkaran. Lengkung pada lingkaran akan terlihat semakin datar jika diperbesar. Pada perbesaran tak terhingga tidak mungkin lagi terlihat perbedaan antara lengkung lingkaran dengan garis lurus. Fraktal tidak seperti ini. Ide konvensional kurvatur, yang merupakan resiprokal dari jari-jari lingkaran aproksimasi, tidak bisa digunakan. Pada fraktal, meningkatkan perbesaran akan menunjukkan detail yang tidak terlihat sebelumnya.
Beberapa contoh fraktal yang umum adalah himpunan Mandelbrot, fraktal Lyapunov, himpunan Cantor, segitiga Sierpinski, karpet Sierpinski, spons Menger, kurva naga, kurva Peano, dan kurva Koch. Fraktal bisa deterministik maupun stokastik. Sistem dinamikal chaotissering (bahkan mungkin selalu) dihubungkan dengan fraktal.
Benda-benda yang mendekati fraktal bisa ditemukan dengan mudah di alam. Benda-benda tesebut menunjukkan struktur frakral yang kompleks pada skala tertentu. Contohnya adalah awan, gunung, jaringan sungai, dan sistem pembuluh darah.
Harrison (Inggris) [1] meluaskan kalkulus Newtonian ke domain fraktal, termasuk teorema Gauss, Green, dan Stokes.
Fraktal biasanya digambar oleh komputer dengan perangkat lunak fraktal. Lihat daftarnya di bawah.
Fraktal acak memiliki kegunaan praktis yang terbesar sebab dapat digunakan untuk mendeskripsikan banyak benda di alam. Contohnya adalah awan, gunung, turbulensi, garis pantai, dan pohon. Teknik-teknik fraktal juga telah digunakan pada kompresi gambar fraktal dan berbagai disiplin sains.












Ulasan
Catat Ulasan